기타의 액션

오랫만에, 오랫동안 망설이다가 이 글을 올립니다.

제가 망설인 이유는 우선 필요한 그림을 그릴 시간적 여유도 없었거니와, 무엇 보다도 이 글의 내용이 순전히 이론에만 의존한 것으로 실험을 통하여 입증 된 것이 아니기 때문입니다. 이런글 올렸다가 누구처럼 돌 맞는것 아닌가 싶기도 하고... 그러나 전 어디까지나 아마추어 이므로, 아마추어리즘을 방패(?)로 삼아, 그래도 혹 관심있는 분들께 더 좋은 아이디어를 가질수 있는 기회가 될까하여 올려봅니다.

(여기서 사용한 용어는 대부분 제가 만든 것이므로 표준이 아닙니다.)

* * * * * *

저는 특히 손이 작고 힘도 약하여 장력이 강한 기타는 말 그대로 아주 쥐약입니다. 그러나 불행하게도 제 기타는 액션이 높아 장력도 엄청 세고, High Position으로 가면 그야말로 고공 줄타기하는 기분이 들 정도지요. 그러다 보니 기타를 치고 싶어도 손이 잘 안가게 되고… 솔직히 이런 기타는 치려면 좀 짜증이 납니다.

이제까지는 그저 제 손힘이 약하고 무엇보다도 실력이 딸려서 그려려니 생각 했는데 전에 수님의 글에서 그런 기타는 전문연주가들에게 조차도 연주가 불가능할 정도라는 사실을 알고 기타의 연주를 편하게 할수 있는 액션에 대하여 좀더 구체적으로 생각하게 되었습니다.

그래서 이글의 주제는 제가 예전부터 생각해왔던 지판의 곡률에 관한 이야기 입니다. 혹시 수학에 앨러지가 있는 분에게는 따분한 글이 되겠습니다마는... (^^)


지판의 곡률을 말하기전에 잠깐 평균률과 프렛의 위치에 관해 언급해야 할것 같습니다. 평균률은 한 옥타브( 주파수비 1:2)을 12개의 동일한 반음정으로 나눈 것이므로 반음의 주파수비는 1:2^(1/12) – 즉, 1대 2의 1/12제곱, 또는 2의 12 제곱근이 됩니다. (글로 수식을 표현하기가 좀 거시기 하네요.) 현의 길이는 주파수와 반비례하므로 현장의 비율로 보면 반음이 올라갈 때 현장은 2^(-1/12)로 짧아지는데 이는 17/18과 거의 근사하므로(17/18=.094444, 2^(-1/12)=0.943874) 제작가들은 남은 현의 길이에서 1/18 위치마다 다음 프렛을 박아 나가기도 합니다.

여기서 액션을 결정하는 요인은, 어느 프렛을 짚었을때 버징이 안나려면 다음 프렛과 현의 간격이 얼마나 떨어져야 하는가 입니다. 일반적으로는, 아니 제가 본 바로는 거의 모든 경우 지판은 현과 약간의 각도를 갖는 직선으로 되어있고 경우에 따라서는 1,2 프렛만 약간 높이는 것으로 보입니다. 물론 지판을 곡선으로 만드는 제작가도 있기는 하지만 그 곡선이 뚜렷하게 어떤 곡선인가는 분명하지 않습니다.

* 참고: http://www.sempleguitars.com/making/action.htm – 여기서는 정현파(Sine Wave) 곡선을 말하는것 같은데 과연 정현파 곡선이 지판의 곡률로서 적합한지는 다음에 언급하겠습니다.
또 갈매기 날개형(~을 뒤집은 모양)의 지판을 주장하는 것도 보았지만 근거가 약해 보입니다.

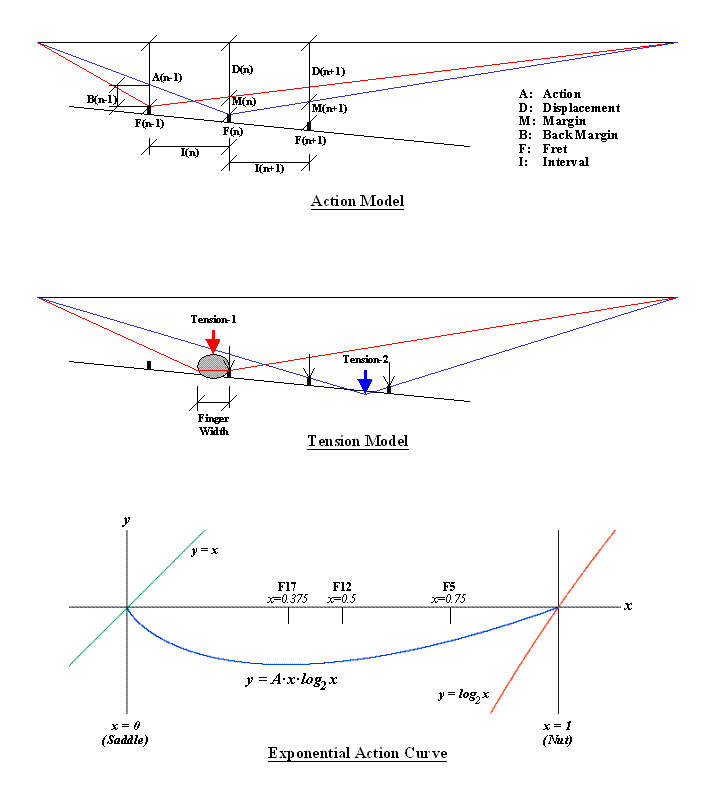
그림 [Action Model]은 현과 프렛간의 거리를 나타냅니다. 프렛 F(n-1)을 누른 경우가 빨간 선으로 표시되어있고 프렛 F(n)을 누른 경우가 파란 선입니다. 현과 프렛의 간격 A(Action)을 두가지의 요소로 분리 하였는데 하나는 그 앞의 프렛을 눌렀을때 현이 프렛에 접근하는 변위 D(Displacement)와 그 때의 현과 프렛의 간격 M(Margin)입니다. 이 마진이 버징을 피하는 최소값을 유지해야 합니다. B(Back Margin)은 뒤쪽으로의 마진, 즉, 5번 프렛을 짚었을 경우 현이 4,5 프렛에 걸리므로 3번 과의 마진을 말합니다. 실제로 이 Back Margin이 너무 낮은 경우 버징의 주된 원인이 되므로 중요하게 고려할 요소 입니다.

우선 Displacement는 앞 프렛에서의 액션과 그 위치에 의하여 결정됩니다. F(n)과 F(n+1)의 거리(Interval) I(n+1)은 앞서 말한대로 현장의 2^(-1/12), 편의상 17/18로 보면, D(n+1) = (17/18) * A(n), 즉, 이전 프렛의 액션에서 17/18의 비율로 접근하게 됩니다. 그리고 그 마진도 앞 프렛에서 필요한 마진의 17/18만 있으면 됩니다. (현장이 줄어들게 되면 그 진폭도 비례하여 줄어 든다는 전제하에 – 진폭과 주파수, 파의 에너지 관계는 또 다른 얘기가 되므로 여기서는 생략합니다.) 따라서 다음 프렛에서의 액션 A(n+1) = D(n+1) + M(n+1)인데, 이때 D(n+1) = (17/18) * A(n), M(n+1) = (17/18)* M(n)이 됩니다. @#$%…!!!

제가 써놓고 봐도 먼 소린지 모르겠네요. (>.<) 그럼 예를들어 쉽게 설명해 보겠습니다.

1번 프렛의 액션, 즉 개방현에서 현과 1번 프렛의 거리가 1mm 였다고 합시다. 그런데 1번 프렛을 짚으면 현장은 17/18로 짧아 지고 현은 2번 프렛으로 1 * (17/18) = 0.944mm 접근하게 됩니다. 이때 2번의 마진은 1번에서의 마진 1mm의 17/18이 필요합니다. (현장이 짧아지면 진폭도 비례해서 작아지므로) 따라서 2번의 마진은 1 * (17/18) = 0.944mm가 필요하고 결국 2번 프렛에서의 액션은 Displacement + Margin = 0.944 + 0.944 = 1.889mm가 됩니다. 그리고 이것이 계속 반복되며 다음 프렛에 적용 됩니다. (수열로 보자면 1, 2 * (17/18), 3 * (17/18)^2, 4 * (17/18)^3, …)

이것을 일반식으로 표현하면,

A(n) = A(0) * n * (R^n)

n = Fret Number
R = 1/(2^(1/12))
A(0) = Fret#0에서의 액션(???)

* 0번 Fret (Nut)에서의 액션이라구요? 물론 그런건 실제로 존재하지 않지만 수식을 간단하게 하기위해 가상적으로 만든 것 입니다. 그 값은 A(12)/6 (12 프렛에서의 액션의 1/ 6) 입니다.

그림 [Tension Model]은 현이 프렛에 닿도록 누르는데 필요한 장력을 말합니다. Tension-1은 손가락의 폭을 일정하게 보고 현을 프렛의 끝에 살짝 대는데 필요한 최소장력을 계산한 모델이고 Tension-2는 현이 앞뒤 양쪽 프렛이 닿도록 하는데 필요한 최소장력의 계산 모델 입니다. (사실 '장력'이라는 용어보다는 '압력'이라는 용어가 더 정확할 것입니다.) 그 숫자의 의미나 값들은 다음에 액셀 파일을 덧붙이겠습니다.

위 수식을 곡선으로 표현하기 위하여 y의 x 함수로 바꾸면,
(Scale Length=1로 간주하고, x = 2 ^ (-n/12) 으로부터)

        y = 12 * A(0) * x * log2(x)

(log2(x) = 2를 base로한 로그 함수)

재미없는 수식에 대해서 더 말하기보다 그러한 곡선이 어떤 모양을 갖는지 보는게 좋겠지요? 그 곡선의 모양은 그림 [Exponential Action Curve]에 있습니다. (A값은 임의로 준 것입니다.) 여기서 x=0는 새들 위치이며 x=1은 너트입니다. 즉, 새들이 왼쪽, 너트가 오른쪽 입니다. 지판, 엄밀히 말하자면 프렛의 선단을 연결한 선은 바로 이러한 곡선을 따라야 한다는 것입니다.

이 그림으로부터 알수 있는 것은 낮은 프렛 (상현주)쪽의 지판은 직선에 가까울 정도로 곡률이 낮지만 높은 프렛으로 오면서 점차 곡률이 높아지며 휘어져 17프렛 (현의 3/8 위치)에서는 지판이 개방현과 평행을 이루는 곡선을 그린다는 것입니다. 앞서 언급한 직선 지판에 상현주 쪽을 약간 높인 것과는 곡률이 반대입니다.

그럼, 과연 이런 곡선을 따른 지판과 직선 지판과의 차이는 무엇일까요? 실제로 눈으로 보아 차이를 거의 느끼지도 못할 만큼의 작은 거리이지만 마진의 배열과 장력에는 현격한 차이를 보입니다. 다시 말해서 직선으로 된 지판은 비합리적인 마진으로 인하여 발생하는 버징을 피하기 위하여 액션을 불필요하게 높여야하고 (특히 상현주) 그 결과로 장력이 증가하여 연주가 어렵게 된다는 것입니다. 이 연구의 목적은 액션의 합리적인 배열로 이를 피하고자 하는 것 입니다.

어쩌다가 드물게 볼수있다는, 액션이 낮아 연주가 편하면서도 버징이 안 난다는 기타는 혹시 네크가 (본의 아니게?) 이런 곡선으로 휜것은 아닌가 생각해 봅니다.

실제 계산된 각 프렛에서의 액션, 마진, 장력 등의 수치와 그에 관한 비교검토는 따로 액셀 파일 (Action Calculator)이 필요하므로 다음 글로 올리겠습니다.


[P.S.]

사실 제가 전부터 생각해 왔던 이상적인 지판의 곡선은 프렛에 닿은 현과 지판이 일정한 각도를 유지하는 Spiral Curve 였습니다. 그러나 여기서 말한 곡선은 각도가 아닌 기울기를 기준으로 계산된 근사치라는 사실을 눈치 채신 분들도 계실 것입니다. 그러나 이 곡선을 주장하는 이유는 그 모양도 거의 Spiral Curve에 가깝고 두 곡선의 차이는 충분히 무시할 수 있을 정도로 극히 미미할 뿐만 아니라, 무엇보다도 Spiral Curve는 제가 계산할 수있는 능력이 안된다는 사실입니다. (ㅡ.ㅡ) Spiral Curve 보다는 이 Exponential Curve의 계산이 훨씬 간단하고 실용적일 것입니다.

* 수님에 의해서 게시물 이동되었습니다 (2006-08-06 10:11)